Background: Diagnostic and prognostic models are typically evaluated with measures of accuracy that do not address clinical consequences. Decision-analytic techniques allow assessment of clinical outcomes but often require collection of additional information and may be cumbersome to apply to models that yield a continuous result. The authors sought a method for evaluating and comparing prediction models that incorporates clinical consequences,requires only the data set on which the models are tested,and can be applied to models that have either continuous or dichotomous results VSports手机版. .

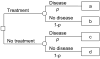
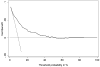
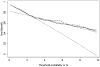
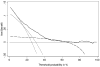
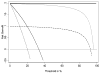
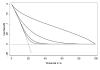
Method: The authors describe decision curve analysis, a simple, novel method of evaluating predictive models. They start by assuming that the threshold probability of a disease or event at which a patient would opt for treatment is informative of how the patient weighs the relative harms of a false-positive and a false-negative prediction. This theoretical relationship is then used to derive the net benefit of the model across different threshold probabilities. Plotting net benefit against threshold probability yields the "decision curve. " The authors apply the method to models for the prediction of seminal vesicle invasion in prostate cancer patients. Decision curve analysis identified the range of threshold probabilities in which a model was of value, the magnitude of benefit, and which of several models was optimal V体育安卓版. .

Conclusion: Decision curve analysis is a suitable method for evaluating alternative diagnostic and prognostic strategies that has advantages over other commonly used measures and techniques. V体育ios版.