Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The . gov means it’s official VSports app下载. Federal government websites often end in . gov or . mil. Before sharing sensitive information, make sure you’re on a federal government site. .

Https

The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely. V体育官网.

. 2006 Jan 15;90(2):400-12.
doi: 10.1529/biophysj.105.069401. Epub 2005 Oct 20.

Swimming in circles: motion of bacteria near solid boundaries

Eric Lauga  1 , Willow R DiLuzio, George M Whitesides, Howard A Stone
Affiliations

Swimming in circles: motion of bacteria near solid boundaries (V体育官网)

Eric Lauga et al. Biophys J. .

Abstract

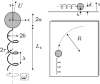
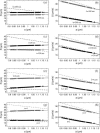
Near a solid boundary, Escherichia coli swims in clockwise circular motion VSports手机版. We provide a hydrodynamic model for this behavior. We show that circular trajectories are natural consequences of force-free and torque-free swimming and the hydrodynamic interactions with the boundary, which also leads to a hydrodynamic trapping of the cells close to the surface. We compare the results of the model with experimental data and obtain reasonable agreement. In particular, the radius of curvature of the trajectory is observed to increase with the length of the bacterium body. .

PubMed Disclaimer

Figures

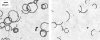
FIGURE 1
FIGURE 1
Superimposed phase-contrast video microscopy images show E. coli cells (HCB437) swimming in circular trajectories near a glass surface. (Left) Superposition of 8 s (240 frames) of video images. (Right) Typical superposition of 2 s (60 frames) of video images that was used to analyze the length and width of cells, the swimming speed of cells, and the radius of curvature of the trajectories.
FIGURE 2
FIGURE 2
Results of our experimental investigation of swimming E. coli near solid boundaries. (Left) Radius of curvature of the circular trajectory, ℛ, as a function of the equivalent sphere radius, a, of the elliptical cell body (see text). (Right) Swimming speed, U, versus equivalent body radius, a. In both cases, we have added as dashed lines the best least-square fit to the data of the form αa + β. (Left) α = 86.78, β = −61.99 μm, and R2 = 0.55. (Right) α = −19.09 s−1, β = 39.39 μm s−1, and R2 = 0.165.
FIGURE 3
FIGURE 3
Setup and notations for the mechanical model of E. coli swimming near a solid surface.
FIGURE 4
FIGURE 4
Physical picture (side and front views) for the out-of-plane rotation of the bacterium: (a) The positive y-rotation of the cell body leads to a net viscous x-force on the cell body, formula image (b) The negative y-rotation of the helical bundle leads to a net negative viscous x-force on the flagella, formula image The spatial distribution of these forces leads to a negative z-torque on the bacterium, which makes it rotate clockwise around the z-axis. Therefore, when viewed from above, the bacterium swims to its right.
FIGURE 5
FIGURE 5
Comparison between the results of the experiments (▹), the full hydrodynamic model (numerical solution of Eq. 11, ▪; and best fit, straight line) and the simplified model (Table 2, dash-dotted line) with a fixed gap thickness h. (Top) h = 10 nm and ω = 156 Hz: (a) radius of curvature, ℛ, and (b) swimming velocity, U, as a function of the bacterial radius a. (Bottom) h = 60 nm and ω = 127 Hz: (c) radius of curvature, and (d) swimming velocity as a function of the bacteria radius a.
FIGURE 6
FIGURE 6
Dependence of the results {ℛ,U} on the geometrical parameters {b, r, λ, n} for the two models (full model: squares and best fit, solid line; approximate analytical model: dash-dotted line), in the case where r = 50 nm, λ = 2.5 μm, b = 250 nm, L‖ = 3 λ (n = 3), h = 30 nm, and ω = 150 Hz, and one of the parameters is varied at a time. (a and b) Dependence on the helix radius, b, for two values: b = 200 nm (▪ and thick lines) and b = 300 nm (□ and regular lines). (c and d) Dependence on the bundle radius, r, for two values: r = 20 nm (▪ and thick lines) and r = 100 nm (□ and regular lines). (e and f) Dependence on the helix wavelength, λ, for two values: λ = 1 μm (▪ and thick lines) and λ = 4 μm (□ and regular lines). (g and h) Dependence on the number of wavelengths, n, for two values: n = 2 (▪ and thick lines) and n = 4 (□ and regular lines).
FIGURE 7
FIGURE 7
Best fit to the experimental data (▹) by an h(a) law in the full hydrodynamic model (numerical solution of Eq. 11, straight line), as given by Eq. 25. The relation between h and a is chosen to obtain the same linear slope for the results of the model and the experimental data (a) and the best least-square difference between the model and the data (b).
See this image and copyright information in PMC

References

    1. Berg, H. C. 2000. Motile behavior of bacteria. Phys. Today. 53:24–29.
    1. Berg, H. C. 2004. Escherichia coli in Motion. Springer-Verlag, New York.
    1. Maeda, K., Y. Imae, J. I. Shioi, and F. Oosawa. 1976. Effect of temperature on motility and chemotaxis of Escherichia coli. J. Bacteriol. 127:1039–1046. - PMC - PubMed
    1. Berg, H. C., and L. Turner. 1990. Chemotaxis of bacteria in glass capillary arrays—Escherichia coli, motility, microchannel plate, and light scattering. Biophys. J. 58:919–930. - "V体育ios版" PMC - PubMed
    1. Frymier, P. D., R. M. Ford, H. C. Berg, and P. T. Cummings. 1995. Three-dimensional tracking of motile bacteria near a solid planar surface. Proc. Natl. Acad. Sci. USA. 92:6195–6199. - PMC - PubMed

Publication types

MeSH terms

LinkOut - more resources